Learning from Reward-Free Offline Data:
A Case for Planning with
Latent Dynamics Models

Vlad Sobal^*1, Wancong Zhang^*1, Kyunghyun Cho^1,2, Randall Balestriero³, Tim G. J. Rudner¹, Yann LeCun^1,4

¹New York University, ²Genentech, ³Brown University, ⁴Meta FAIR
^*Equal contribution, order determined by coin flip,

Overview

Abstract

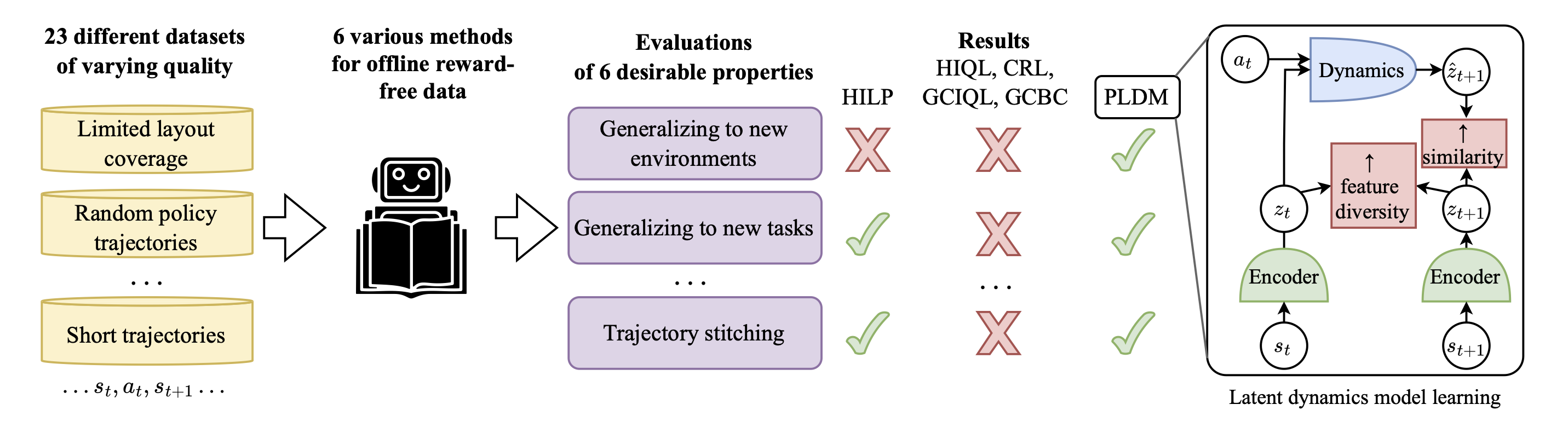
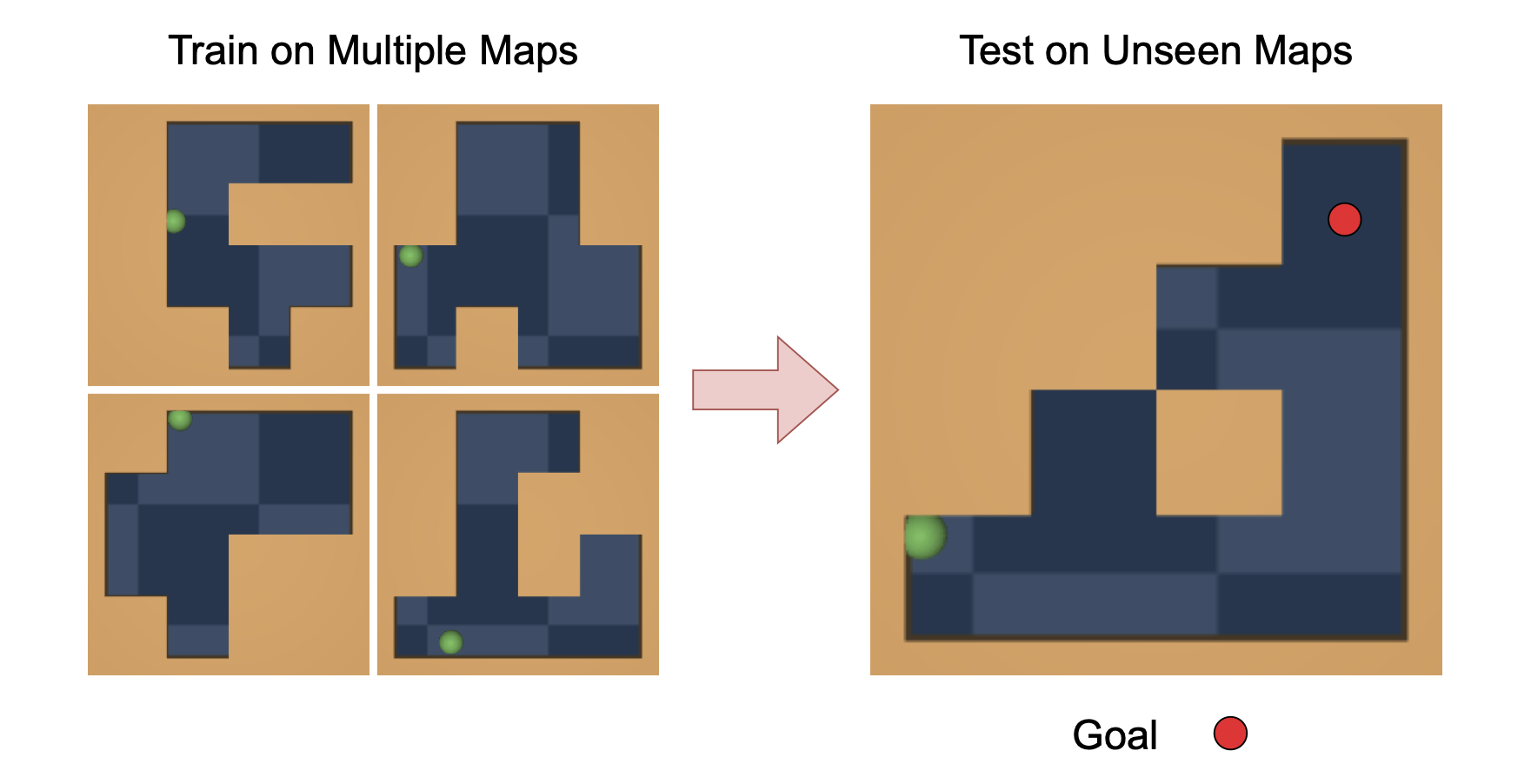
A long-standing goal in AI is to build agents that can solve a variety of tasks across different environments, including previously unseen ones. Two dominant approaches tackle this challenge: (i) reinforcement learning (RL), which learns policies through trial and error, and (ii) optimal control, which plans actions using a learned or known dynamics model. However, their relative strengths and weaknesses remain underexplored in the setting where agents must learn from offline trajectories without reward annotations.

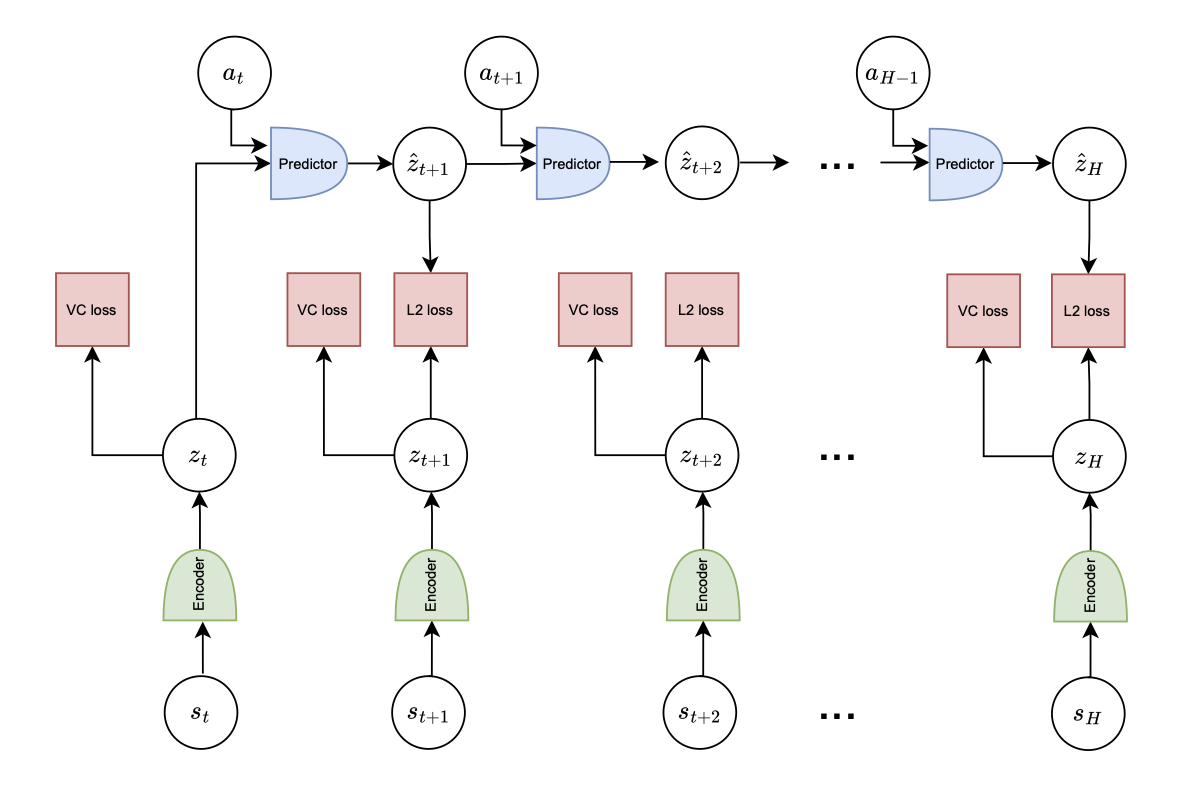
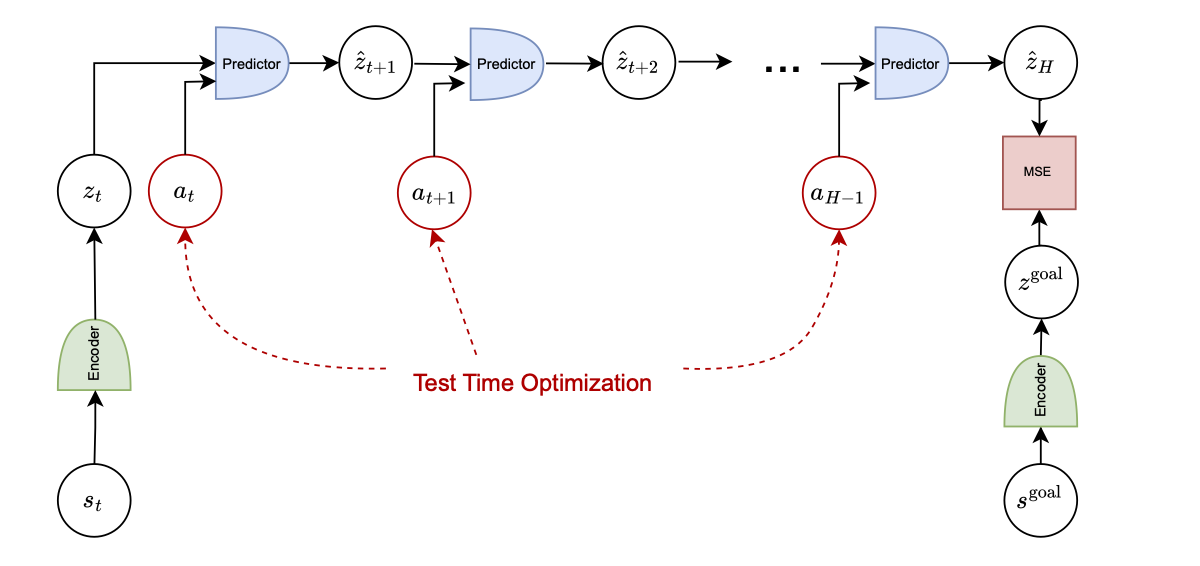
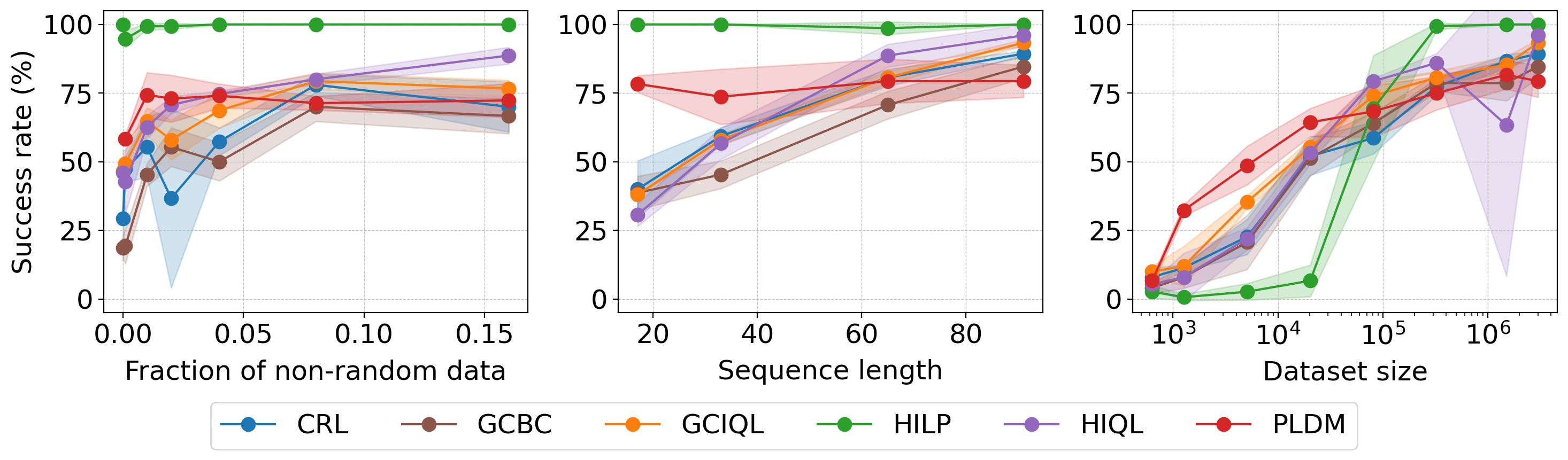
In this work, we systematically analyze the performance of different RL and control-based methods under datasets of varying quality. On the RL side, we consider goal-conditioned and zero-shot approaches. On the control side, we train a latent dynamics model using the Joint Embedding Predictive Architecture (JEPA) and use it for planning. We study how dataset properties—such as data diversity, trajectory quality, and environment variability—affect the performance of these approaches.

Our results show that model-free RL excels when abundant, high-quality data is available, while model-based planning excels in generalization to novel environment leayouts, in trajectory stitching, and data-efficiency. Notably, planning with a latent dynamics model emerges as a promising approach for zero-shot generalization from suboptimal data.

Training and Planning with Latent Dynamics Model

We train a latent dynamics model end-to-end from offline trajectories using the Joint Embedding Predictive Architecture (JEPA). JEPA learns to predict its own future states within the latent space. To achieve this, we minimize the prediction error using an L2 loss and apply Variance-Covariance Regularization (A. Bardes, 2022) to prevent representation collapse.

To plan with the learned latent dynamics model at test time, we encode the goal state, and optimize the actions in order to minimize the distance between the unrolled predictions and the goal state in the latent space.

Environments & Datasets

The task: reach a specified goal in top-down navigation

We present two top-down navigation environments - Two Rooms and Diverse Mazes. In both, the goal is to reach a specified goal state. A typical task for Two Rooms is illustrated on the left. We test algorithms' ability to learn from data of varying quality. On the right is an example trajectory in the offline dataset.

Example Trajectories from the Two Rooms Dataset ... (click to expand)

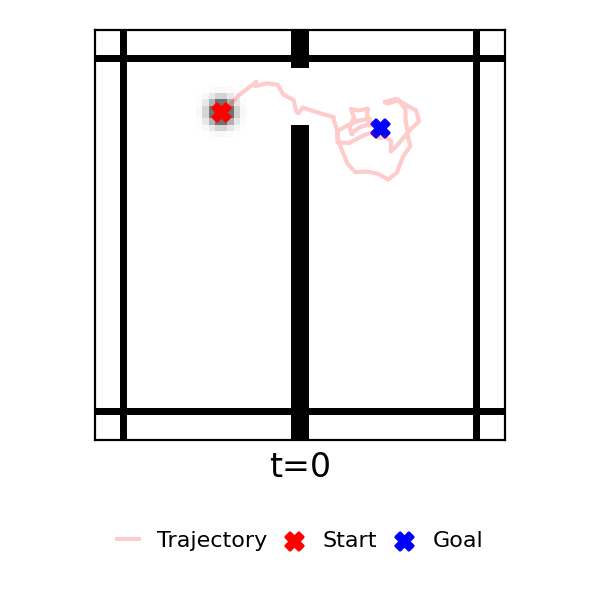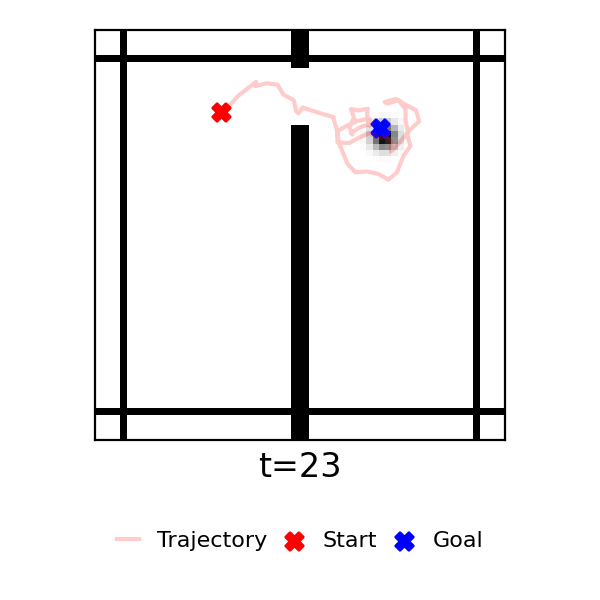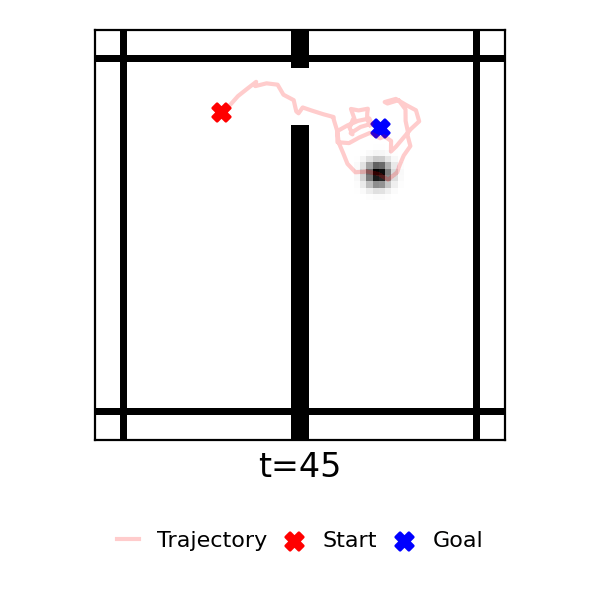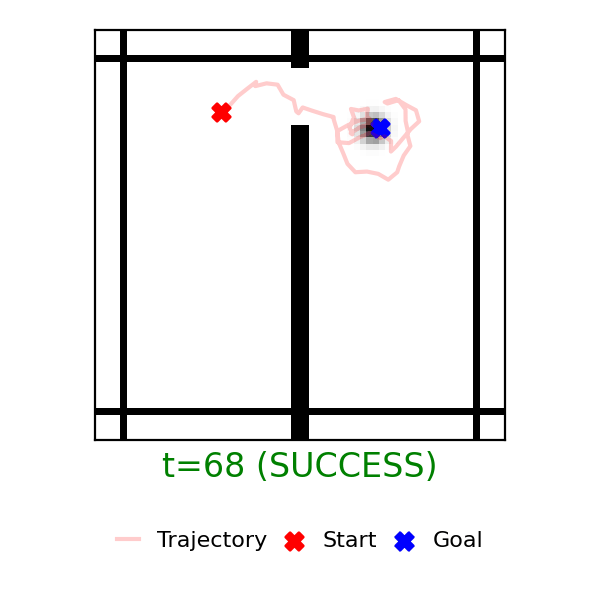
The following GIFs show example trajectories collected in the dataset. These illustrate the variety of movements and behaviors captured in different data settings.

Good quality-trajectories (length=90)

Random policy trajectories

Trajectories of length 16

Trajectories of length 32

Trajectories of length 64

Diverse Mazes: testing generalization to new environments

In our second, more challenging environment, we train the agents on random trajectories of a point mass agent from mazes with different layouts, and evaluate their performance on held-out layouts.

Main Results

Generalization to new environments

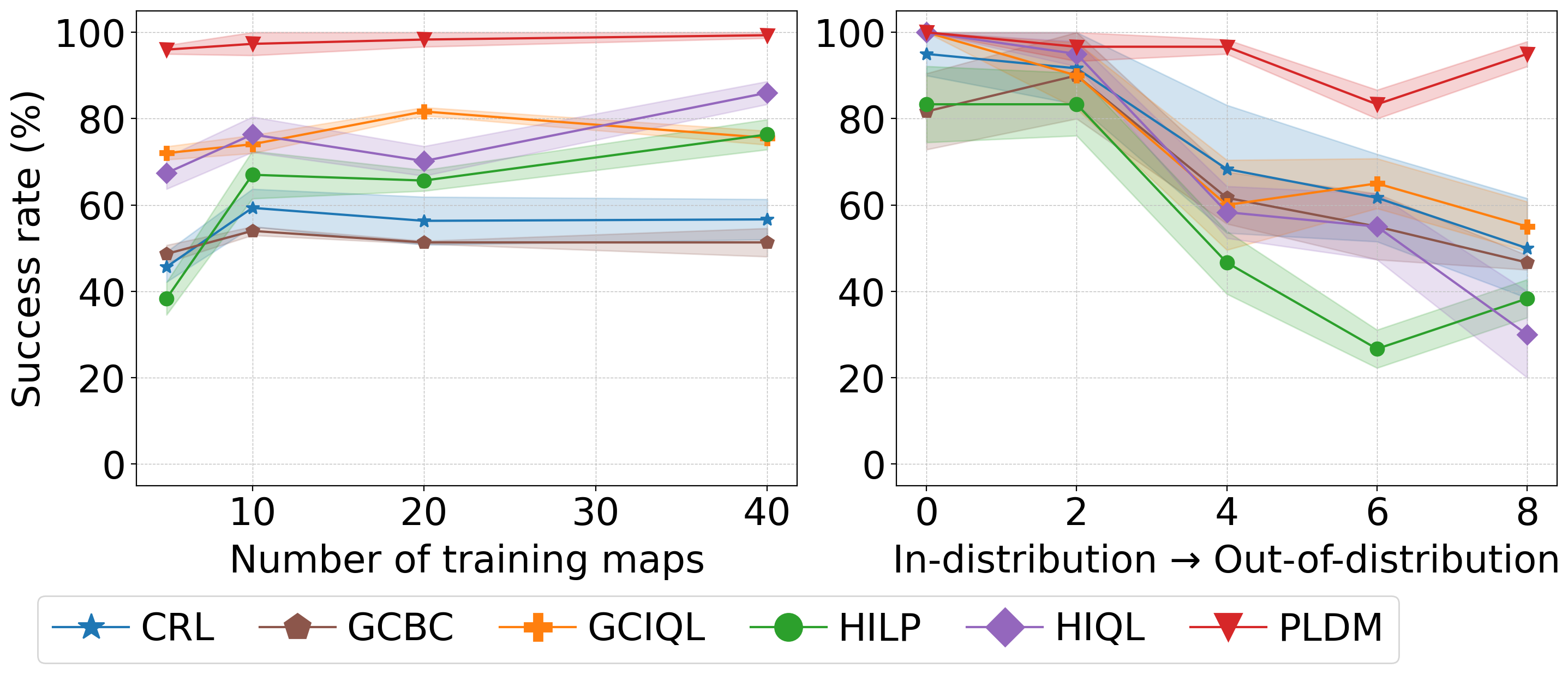
Maze layout evaluation results — **Left:** Success rates of tested methods on held-out layouts, as a function of the number of training layouts. **Right:** success rates of models trained on data from 5 layouts, evaluated on held-out layouts ranging from similar to training layouts to out-of-distribution ones. We use map layout edit distance from the training layouts as a measure of distribution shift. PLDM demonstrates the best generalization. Results are averaged over 3 seeds, shaded area denotes standard deviation.

Low distribution shift

CRL

GCBC

GCIQL

HILP

HIQL

PLDM

Medium distribution shift

High distribution shift

Generalizing from suboptimal training data

Main experiments on two rooms environment. — **Testing the selected methods' performance under different dataset constraints.** Values and shaded regions are means and standard deviations over 3 seeds, respectively.
**Left:** To test the importance of the dataset quality, we mix the random policy trajectories and good quality trajectories. As the amount of good quality data goes towards 0, methods begin to fail, with PLDM and HILP being the most robust ones.
**Center:** We measure methods' performance when trained with different trajectory lengths. We find that many goal-conditioned methods fail when train trajectories are short, which causes far-away goals to become out-of-distribution for the resulting policy.
**Right:** We measure methods' performance with datasets of varying sizes. We see that PLDM is the most sample efficient and manages to get almost 50% success rate even with a few thousand transitions.

Summary

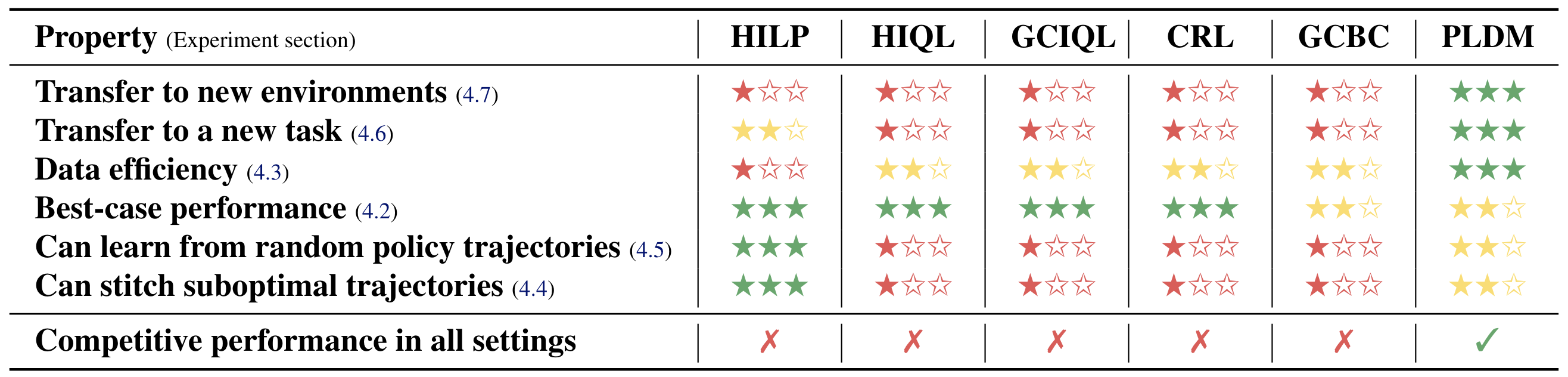
Having thoroughly evaluated six methods for learning from reward-free offline trajectories. The table below summarizes their performance across several key challenges: (i) Transfer to new environments, (ii) Zero-shot transfer to a new task, (iii) Data-efficiency, (iv) Best-case performance when data is abundant and high-quality, (v) Ability to learn from random or suboptimal trajectories, and (vi) Ability to stitch suboptimal trajectories to solve long-horizon tasks.

Comparison table of different methods. — **Table 1:** Summary of each method's strengths and weaknesses in different data conditions and generalization requirements.

Takeaways

Learning a latent dynamics model and using it to plan exhibits robustness to data quality, superior data efficiency, and the best generalization to new layouts and tasks;
Learning a well-structured latent-space (e.g. using HILP) enables trajectory stitching and robustness to data quality, although it is more data-hungry than other methods;
Model-free GCRL methods are a great choice when the data is plentiful and good quality.

BibTeX

@article{sobal2025learning,
  title={Learning from Reward-Free Offline Data: A Case for Planning with Latent Dynamics Models},
  author={Sobal, Vlad and Zhang, Wancong and Cho, Kynghyun and Balestriero, Randall and Rudner, Tim G. J. and LeCun, Yann},
  journal={arXiv preprint arXiv:2502.14819},
  year={2025},
  archivePrefix={arXiv},
}